| Product(s): |
HAMMER |
| Version(s): |
CONNECT Edition, V8i |
| Area: |
Modeling |
Problem Description
What is the purpose of the Transient Friction Method option in the transient calculation options in HAMMER?
What is the difference between Steady, Quasi-Steady, Unsteady and Unsteady-Vitkovsky methods?
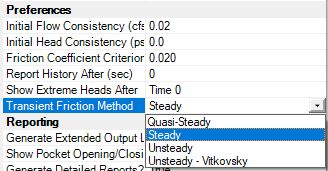
Resolution
The "Transient Friction method" determines how HAMMER changes pipe friction factors during the transient simulation, as the system conditions change.
The default is "Steady" which should work for most modeling cases. "Steady" means that the friction factor calculated from the initial conditions is assumed to be held constant for the entire transient simulation (the Darcy-Weisbach 'f' will not change as transient conditions change).
With the Quasi-steady, Unsteady and Unsteady-Vitkovsky methods, the friction factor (f) for each pipe is continually adjusted (mainly increased) during the simulation as the fluid accelerates and decelerates. With the Quasi-steady method, the friction factor is adjusted such that friction losses for an instantaneous velocity match the friction losses which would occur for fully developed steady flows with the same cross-sectional average velocity. With the Unsteady method, HAMMER can track the effect of fluid accelerations to estimate the attenuation of transient energy more closely than would be possible with quasi-steady friction. See the Help topic (mentioned further below) for more details on the calculation methodology.
Which one should I use?
Based on the above, one can conclude that the unsteady methods may provide more accurate results, though the steady method may be considered more conservative (the smaller the friction losses, the longer it takes to dissipate transient energy.)
Since the steady method is considered more conservative, it is the default option and is likely the best choice for most surge analysis. However if you're trying to calibrate to measured results or need to accurately analyze cyclical fatigue (for example how many times the pressure rises above a certain threshold), then the unsteady method is recommended since it will tend to yield results closer to real field measurements.

"Unsteady" vs "Unsteady-Vitkovsky" Methods
In earlier versions of HAMMER, there was only one "Unsteady" transient friction method available. This method was developed by Brunone et al., 2000; Vardy and Brown, 1995 and Vitkovsky et al., 2000.
However, ongoing research in this area led to an alternative method that HAMMER calls "Unsteady - Vitkovsky", which was developed by Bergant, Simpson and Vitkovsky, 2001.
The exact formulas used for each method are found in the HAMMER help documentation, under Contents > Bentley HAMMER V8i Theory and Practice > Friction and Minor Losses > Transient Analysis Friction Methods > steady or Transient Friction
In general, the "Unsteady - Vitkovsky" transient friction method is now the recommended unsteady friction method for use in HAMMER and should provide more accurate results than the "Unsteady" method. The "Unsteady" method was left in the program for legacy support. Meaning, models that were created in older versions of HAMMER that used this method will still be able to use it, to achieve comparable results in the new version.
If you experience numerical stability problems when using one of the unsteady methods, try the other one, or try adjusting the timestep.
How is the friction factor calculated with each method?
See Help Topics:
- Help > HAMMER Help > Contents > Modeling Capabilities > Calculation Options > Selecting the Transient Friction Method.
- Contents > Bentley HAMMER Theory and Practice > Transient Analysis Friction Methods
Quasi-Steady
In this approach (Fok, 1987), the Darcy-Weisbach coefficient at any point depends on the state of the system at the previous time step. At the outset, the friction coefficient for each pipe is a function of the initial flow, Q0 , as follows: (i) calculated from the steady-state conditions if |Q0 | > 0, or (ii) the user-entered value of the coefficient if Q0 = 0. For the starting value of the friction coefficient, the relative roughness of each pipe is estimated by means of the Swamee and Jain (1976) approximation of the Moody diagram. For subsequent time steps, the Reynolds number is computed at each point on the basis of the previous iteration's velocity and then an updated friction coefficient is ascertained.
The steady-state friction method is actually a special case of the quasi-steady method because it assumes that the friction factor does not vary with time. The quasi-steady friction method is virtually an unsteady method, although one based on steady-state friction factors (c.f. Unsteady or Transient Friction). The quasi-steady method is more computationally demanding than steady-state friction.
Unsteady and Unsteady-Vitkovsky
Compared to a steady state, fluid friction increases during hydraulic transient events because rapid changes in transient pressure and flow increase turbulent shear. Bentley HAMMER V8i can track the effect of fluid accelerations to estimate the attenuation of transient energy more closely than would be possible with quasi-steady or steady-state friction.
It is known that past velocity and/or temporal acceleration play a significant role in determining transient friction (Brunone et al., 1991; Bughazem and Anderson, 2000; Vardy and Hwang, 1991). Motivated by experimental data and published formulae in recent years for estimating the transient friction factor (Brunone et al., 2000; Vardy and Brown, 1995; Vitkovsky et al., 2000), we have proposed an unsteady friction model defined by an amplification of the quasi-steady friction factor by the following factor:
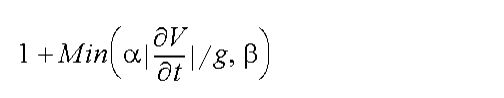
where V is velocity, t is time, g is gravitational acceleration, = 10,000 and = 4 (0) for acceleration (deceleration). The partial derivative of velocity with respect to time is the temporal acceleration at any point and is evaluated at the previous time step. On account of ongoing research in this area, an alternative transient friction method has also been provided (Bergant, Simpson and Vitkovsky, 2001). Selecting "Unsteady - Vitkovsky" as the transient friction method will employ the below formulation:
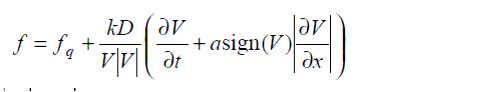
Where f is the Darcy-Weisbach friction factor, fq is the quasi-unsteady component of the friction factor (based on updating Reynolds number for each new computation), D is pipe diameter, V is flow velocity, t is time, a is wave speed, sign(V) is equal to +1 when velocity is greater than zero and -1 when velocity is less than zero, x is distance, and k is Brunone's friction coefficient. The coefficient k can be computed using the following equation:
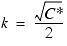
Where C* is Vardy's shear decay coefficient.
For laminar flow C* =0.00476
For turbulent flow 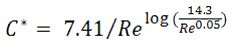
This unsteady friction method from Vitkovsky is now the recommended unsteady friction method for use in HAMMER.
Computational effort increases significantly if transient friction must be calculated for each time step. This can result in long model-calculation times for large systems with hundreds or pipes or more. Typically, transient friction has little or no effect on the initial low and high pressures, and these are usually the largest ever reached in the system. This is illustrated from the following Bentley HAMMER CONNECT simulation results comparing steady, quasi-steady and transient friction methods.

Figure 14-11: Bentley HAMMER CONNECT Results for Steady-State, Quasi-Steady, and Transient Friction Methods
The steady-state friction method yields conservative estimates of the extreme high and low pressures that usually govern the selection of pipe class and surge-protection equipment. However, if cyclic loading is an important design consideration, the unsteady friction method can yield less-conservative estimates of recurring and decaying extremes.
For the initial pressure rise or decline, the various models yield results which are nearly identical to each other, as well as to empirical data. As time passes, however, the match progressively deteriorates for subsequent peaks and valleys especially when the flow changes are more abrupt as illustrated above. The usual convex velocity profile in steady state begins to break down when the flow is rapidly varied with regions of flow recirculation, flow reversal and increased intensity of turbulence (Brunone et al., 2000). Thus, the fundamental assumption of one-dimensional flow is severely strained. Although the unsteady model, in particular, matches the empirical decay in amplitude quite well, it fails to account for the attendant change in the shape of the wave with increasing time. The topic of unsteady friction remains in the forefront of hydraulics research.
See Also
Transient pressure wave not dampening or unexpected lack of headloss