| |
Applies To |
|
|
| |
Product(s): |
HAMMER |
|
| |
Version(s): |
08.11.XX.XX and higher |
|
| |
Area: |
Modeling |
|
| |
Original Author: |
Scott Kampa, Bentley Technical Support Group |
|
Overview
This Technote provides a reference for modeling transients with turbines in HAMMER, for hydropower applications. Additional information can be found in the Help documentation for the product.
For information on modeling turbine energy recovery in WaterCAD or WaterGEMS, see: Using the Scenario Energy Cost and Energy Management tools in WaterGEMS and WaterCAD
For a training video and workshop see part 16 of the HAMMER training course.
Background
Turbines are used to convert the potential energy of flowing water into electricity. They can be used in large scale applications like dams, or small scale such as recovering energy on the downstream side of a hill.. Given the importance of turbines in these systems, it is essential for a modeler to predict the transient pressures that might occur for example as a result of sudden closure of the wicket gate (to prevent overspeed) and to implement an adequate surge control strategy to ensure the safety and reliability of the turbine.
HAMMER can be used to model transient simulations where turbines are involved and analyze potential protective measures that can be used to mitigate the effects of transient events.
Turbines in HAMMER
Hydropower turbines are located at the downstream end of a conduit, or penstock, to absorb the moving water's energy and convert it to electrical current. Conceptually, a turbine is the inverse of a pump, but very few pumps or turbines can operate in both directions without damage. If the electrical load generated by a turbine is rejected, a wicket gate (which is built into the turbine element in HAMMER) must rapidly stop flow, resulting in a large increase in pressure, which propagates upstream (in the penstock).
Note: HAMMER currently does not support modeling a pump-turbine element - see more at the bottom of this article.
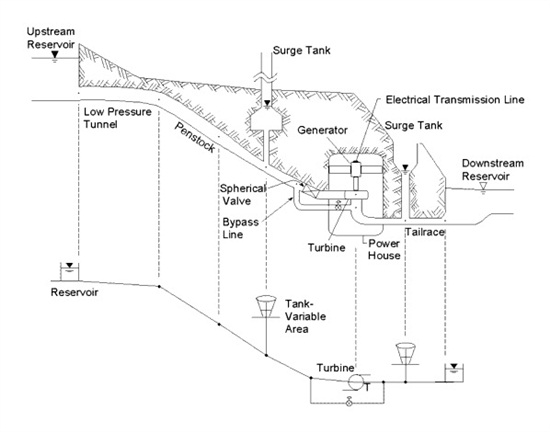
The primary purpose of transient simulations with turbines is to look at ways to protect the system against rapid changes in the electrical and/or hydraulic components of the hydroelectric system. In each case, hydraulic transients result from changes in the variables controlled by the governor.
Electrical Load or Torque on the turbine-generator system varies with the electrical load in the distribution grid. In steady-state operation, the electrical torque and the hydraulic torque are in dynamic equilibrium. From a hydraulic perspective, electrical torque is an external load on the turbine.
The moment of inertia comes into play here as it can influence the rate at which a turbine speeds up or slows down. See further below for an explanation of how HAMMER calculates the turbine speed change.
What value should I use for moment of inertia of a turbine? Should I use WR^2 or GD^2?
Moment of inertia in HAMMER is defined by the equation WR^2, where W is the weight of the turbine and R is the "radius of gyration" (not the radius of the impeller). Reference.
Moment of inertia is related by torque by way of the following equation:
I*d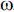 /dt = M
/dt = M
where:
I is the moment of inertia, which is a constant
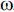 is the rate at which the turbine is spinning (measured in radians per second)
is the rate at which the turbine is spinning (measured in radians per second)
d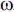 /dt is the rate of change in (omega) over time (radians per second per second)
/dt is the rate of change in (omega) over time (radians per second per second)
M is the net torque applied to the turbine (i.e., the difference between the torque from the water that is spinning the turbine and the torque from the generator that the turbine is attached to).
So if M = 0, then the hydraulic and electrical torque is balanced, and the turbine speed doesn't change (d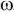 /dt = 0)
/dt = 0)
But if the electrical torque drops to zero, such as in a load rejection operating case, then M becomes greater than zero and the turbine starts to speed up. It will speed up quickly if it has a small moment of inertia, and it will speed up less quickly if it has a large moment of inertia.
Speed is another possible control variable for numerical simulations. For turbines, however, the governor keeps the turbine at synchronous speed by varying the wicket gate position during load variation and acceptance (assuming a 'perfect' governor). If field data were available, the speed could be used to determine whether the model simulates the correct flow and pressures.
Once the time-varying electrical torque and wicket gate positions are known, HAMMER solves flow, Q, and rotational speed, N, in conjunction with the characteristic curves for the turbine. This yields the transient pressures for the load rejection, load acceptance, emergency shutdown, operator error or equipment failure.
As for how the speed change is calculated - During the transient simulation, turbine performance curves are extended by means of the similitude relations along curves of constant efficiency. In effect, in this way HAMMER covers the entire range of values of speed, head, flow, and power for a particular gate position. As gate positions change during load rejection, interpolation between adjacent input gate openings is performed. For load rejection, the accelerating torque drives the increase in rotational speed which is handled by the dynamic conservation of angular momentum equation. Simultaneously, hydraulic transients are modeled via the method of characteristics. In summary, the engine combines all of the foregoing – extended curves at all gate positions, rotational speed increase, head rise, et al. – to represent the transient behavior of the turbine, penstock and tailrace.
The possible emergency or transient conditions are discussed separately in the sections that follow.
Note: The turbine element in HAMMER is not used to represent impulse turbines. Transients caused by impulse turbines can be approximated in HAMMER by using a Throttle Control Valve (TCV) or Discharge to Atmosphere element to represent the turbine nozzle.
How do I model the Draft Tube?
In the above first illustration, this is simply the pipe immediately downstream of the turbine. You can model it as a pipe going to a reservoir, sometimes with a surge tank between.
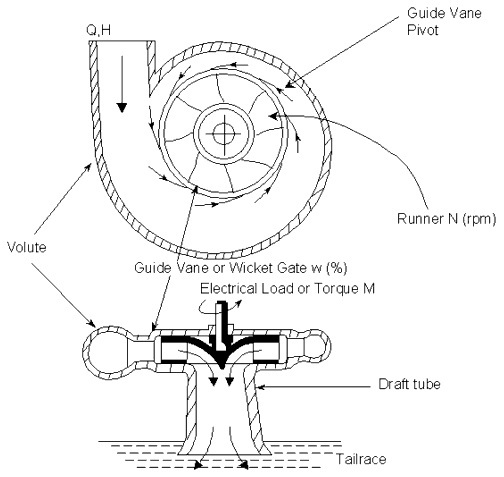
How do I model a bypass valve?
In some cases the turbine may have a built-in "synchronous bypass valve" which opens as the wicket gates close, to help prevent damaging transients.
This can be modeled with the Throttle Control Valve (TCV) element. You would need to manually control the open and closure of the bypass valve using the TCV's operating rule pattern. Here is an illustration of the plan view layout:
The TCV's closure characteristics can be based on either headloss coefficients or discharge coefficients. For more information on TCV modeling, see: Modeling Reference - Valve Closure
You may need to use a smaller timestep to prevent excessive adjustment to the length or wave speed of the two short pipes adjacent to the turbine and TCV, unless you can neglect such adjustments (see this for more).
Although the bypass valve may help keep the water column moving to avoid damaging transient pressures, you would still want to analyze this in HAMMER to confirm. You may also want to consider modeling the case of the bypass valve being stuck, to see what would happen if it did not open as the wicket gates close.
Turbine Properties
Time (Delay until Valve Operates): The period of time that must elapse before the spherical valve of the turbine activates. This should be set to a large value if it will not impact the operation of the turbine.
Time for Valve to Operate: The time required to operate the spherical valve. By default, it is set equal to one time step. This should be set to a large value if it will not impact the operation of the turbine.
Pattern (Gate Opening): Enables you to define the wicket gate closure over time, via the Patterns manager. It consists of the table of time vs. relative gate opening. The relative gate opening is the %open of the wicket gate. Typically for an instant load rejection the wicket gate will start closing at time zero (immediately after the load rejection), but you can also introduce a delay to the start of the closure by setting the relative gate opening to 100% in the first row of the table (with the corresponding time of delay). See the Turbine sample file included with HAMMER for an example of this.
Operating Case: Allows you to choose among the four possible cases: Instantaneous Load Rejection, Load Rejection (requires torque/load vs. time table), Load Acceptance, and Load Variation.
Diameter (Spherical Valve): The diameter of the spherical valve.
Efficiency: The efficiency of the turbine as a percentage. This is typically shown in the curves provided by the manufacturer. A typical range is 85% to 95%, but values outside this range are possible. See below wiki solution for more on turbine efficiency:
http://communities.bentley.com/products/hydraulics___hydrology/w/hydraulics_and_hydrology__wiki/turbine-efficiency.aspx
Moment of Inertia: This value will account for the turbine, generator, and entrained water. This is also typically provided by the manufacturer. As mentioned in the previous section, Moment of inertia is HAMMER is defined by the equation WR^2, where W is the weight on the turbine and R is the radius of gyration.
Speed (Rotational): The rotation of the turbine blades per unit time, typically as rotations per minute or rpm. The power generated by the turbine depends on this value.
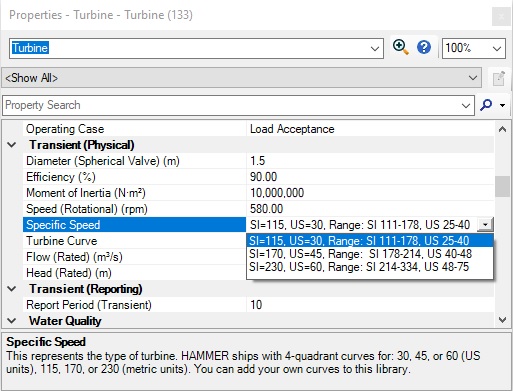
Specific Speed: Enables you to select from a list of available Specific Speeds, which represent a characteristic curve (see further below) that is used to model the hydraulics of the turbine during the transient simulation. The following default specific speeds are included: 30, 45, or 60 (U.S. customary units) and 115, 170, or 230 (SI metric units). The source of these three defaults is the US Bureau of Reclamation. You can enter your own data in the XML library. See the Help documentation for more information.
Note: Starting with HAMMER CONNECT Edition Update 3 (version 10.03.02.75), the specific speed range is presented in the Specific Speed property field for Properties and FlexTables.
Turbine Curve: This curve is used to define the flow and head for the turbine in the initial conditions computation, corresponding to the fully open position of the wicket gate. For a transient run, HAMMER uses a characteristic curve based on Specific Speed, Rated (initial) Head, and Rated (initial) Flow. See more on this below.
Flow (Rated): Denotes the flow under normal operating conditions. Only applies to the Load Acceptance operating case.
Head (Rated): Denotes the headloss through the turbine under normal operating conditions, corresponding to the rated flow. Only applies to the Load Acceptance operating case.
Electrical Torque Curve: defines the time vs. applied (electrical) torque response for the turbine. Only applies to the Load Rejection operating case.
Configuring Turbine Parameters
This section provides additional information on configuring turbine parameters. The exact information entered will vary based on the turbine and the modeling case that is being used.
Initial Conditions Configuration
The properties fields “Operating Case” and “Pattern (Gate Opening)” go hand-in-hand, and are the primary modeling usage for a turbine. More details can be found in the next section. There are four operating cases to choose from: Load Rejection, Instant Load Rejection, Load Acceptance, and Load Variation. The pattern is created in the section “Operational (Transient, Turbine). It used in conjunction with this will represent the relative wicket gate opening at the time from the start of the simulation.
The property field “Turbine Curve” is used to determine the relation between flow and head during the steady state analysis used for the initial conditions. If you are modeling a Load Acceptance operating case, you will need to manually enter a rated flow and rated head instead of the turbine curve. This is so that the program has a starting point for the development of the characteristic curve (based on the shape of the curve specified by way of the Specific Speed selection.) In the other modeling cases, the flow and head used are derived from the turbine curve in the initial conditions. Load Acceptance assumes that the initial status of the turbine is closed, meaning there is no rated flow and head results. Instead, the program will use the rated flow and head entered in the properties.
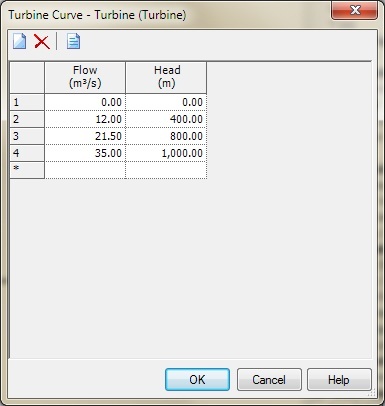
The relationship here is typically the reverse of a pump. Meaning, as flow increases, head increases. This is because the "Head" in this case is not the head added, but rather it is the head drop across the turbine (difference between downstream and upstream HGL) during the initial conditions, some of which will be converted to electrical energy.
The flow and head relationship defined in the Turbine Curve is only used to establish the initial conditions operating point of the turbine and is not used directly during the transient simulation. The transient simulation uses a separate characteristic curve based on the selection of "Specific Speed". The specific speed's characteristic curve defines the shape of the turbine characteristics for each position of the wicket gate (since the wicket gate is built into the turbine) and it applies that dimensionless shape to the set of head and flow from the initial conditions (based on the turbine curve) to establish the characteristic curve used to simulate the turbine during the transient simulation. In other words, the points on the constructed curve are relative to the initial conditions operating point (head/flow) which is derived from the turbine curve.
Since load rejection and variation events assume the wicket gate starts fully open, the Turbine Curve that you enter (for the initial conditions) should represent the turbine's rated/nominal characteristics when the gate is in the fully open position. Meaning, when using the load rejection or load variation operating case, HAMMER assumes that the turbine begins in the fully open position. This assumption should be acceptable for the purposes of a transient simulation where you are typically looking at worst-case conditions.
For load acceptance, the gate is assumed to be initially fully closed. Since the flow is zero, you would enter the "rated" head and flow input fields instead of the turbine curve, and they would also represent the nominal operating point of the turbine when the gate is fully opened (since the wicket gates will open during the transient simulation). This information should be available from the turbine manufacturer or you can obtain it by performing a steady state initial conditions run with the turbine open, and note the calculated head and flow (then close the turbine and enter those values for the nominal operating point for load acceptance). See more in the load acceptance section further below.
If you want to force a specific flow and head for your turbine's initial conditions, there are some options:
1) Enter a minimum number of points on the turbine curve, all close to the desired operating point
2) Use the "specify initial conditions" calculation option. This is a rarely used, legacy feature that allows you to manually specify the initial conditions, instead of allowing the initial conditions steady state solver to calculate them for you. For most models this is not a feasible approach, but if your turbine model is relatively small, it may be worth considering. To do this, open your calculation options under Analysis > Calculation Options > Transient Solver. At the bottom of the list you will see an option called "Specify Initial Conditions". Set this to true to expose various "initial" fields in the properties of your elements. For example for your pipes, you will see a "Flow (Initial)", "Hydraulic Grade (Initial Start)" and "Hydraulic Grade (Initial Stop)". By way of the initial flow and hydraulic grade in the pipes adjacent to the turbine, HAMMER will know what the initial operating point is and will use that for the transient simulation (along with the other parameters like the specific speed). Extra care needs to be taken with this approach, but you won't need to enter an accurate "turbine curve" (though you may need to enter some values in the turbine curve to avoid a validation message, even though the curve won't be used with the calculation option set to True).
Known issue in 10.04.00.108 with 2.2 solver version: Please note that there is a known issue when using the 2.2 solver version (in the Engine Compatibility calculation option) for the initial conditions, which may not properly utilize the turbine head vs. flow curve. To resolve this, change the Engine Compatibility option to the 2.0.12 solver version. This should be resolved in higher versions. See more here.
Transient Simulation Configuration
The specific speed can be estimated with the following equation:
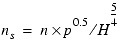
In US units n is in rpm, P is in hp, and H is in ft.
In SI units n is in rpm, P is in kW, and H is in m.
See also: Estimating the Specific Speed of a Pump or Turbine
There are three different default specific speeds available to choose from, obtained from the USBR: “SI=115, US=30,” “SI=170, US=45,” and “SI=230, US=60.”
Note: In a case where you need to use a characteristic curve not represented by the choices above, it is possible to create a custom Specific Speed (and underlying characteristic curve). Please see the Help topic “Pump and Turbine Characteristics in Bentley HAMMER” for details. Note that the data that you enter for the curve is unitless - it represents the shape of the curve, which is applied to the initial head drop and flow across the turbine to construct the characteristics curve (with units) used during the simulation. Note that this information may be difficult to obtain, as a separate curve needs to be entered for each position of the built-in wicket gates.
Lastly, the property field “Report Period (Transient)” will allow the user to see the turbine results in the Transient Analysis Detailed Report. These results will include the time, the gate opening percentage, flow, speed, and head.
Note: the lowest wicket gate position defined in the default characteristic curves for turbines is 20% open. Because of this, HAMMER will not display output information during times when the wicket gate is between 0% and 20% open. Internally, HAMMER linearly interpolates from the flow at 20% open down to zero flow (at the time when the operating rule says the wicket gates are 0% open). See: Why do turbine extended transient results stop at the time when the gate is 20% open?
Modeling cases with Turbines
Like pumps, there are specific operating cases that can be modeled with a turbine in HAMMER. Below is a brief description of each case. There is a sample model which uses each case below. The sample model can be found at C:\Program Files (x86)\Bentley\HAMMER8\Samples\Turbine_Example.wtg.
Instant Load Rejection
Instant Load Rejection is similar to the Load Rejection case, except the electrical load on the turbine drops instantaneously to zero (i.e. the turbine is disconnected from the generator).
Load rejection occurs when the distribution grid fails to accept electrical load from the turbine-generator system. The "Instant" Load Rejection Operating case simulates this by dropping the electrical torque to zero instantly at the start of the simulation. After the load is rejected by the grid, there is no external load on the turbine-generator unit and the speed of the runner increases rapidly. This can be catastrophic if immediate steps are not taken to slow and stop the system. To keep the speed rise within an acceptable limit, the wicket gates (simulated inside the turbine element) must close quickly and this may result in high (followed by low) hydraulic transient pressures in the penstock. Since load rejection usually results in the most severe transient pressures, it typically governs the design of surge control equipment.
A balance must be found between the speed rise and the pressure envelope. The wicket gates must be closed gradually in order to prevent damaging surge pressures, but fast enough to prevent a damaging rise in turbine speed. In a real turbine a governor would control the wicket gate closure rate, however the turbine governor is not modeled explicitly in HAMMER and the user controls the rate of wicket gate closure.
Note: the wicket gate pattern must begin at 100% open and decrease to 0%. If you need to model an instant load rejection with the wicket gate starting less than 100% open, see this article: Modeling turbine instant load rejection with wicket gate starting less than 100% open
As gate positions change during load rejection, interpolation between adjacent input gate openings is performed. For load rejection, the accelerating torque drives the increase in rotational speed which is handled by the dynamic conservation of angular momentum equation. Simultaneously, hydraulic transients are modeled via the method of characteristics.
Load Rejection
The Load Rejection operating case is similar to the Instant Load Rejection case, except you can define a pattern of electrical torque over time rather than assuming it drops to zero in the first timestep. The speed of the turbine will then react accordingly based on the inertia and hydraulic conditions, and the closure rate of the wicket gate pattern. See the above description of instant load rejection for more information.
If the power generated by the water flowing through the turbine (hydraulic torque) is greater than the electrical load (electrical torque), then the turbine will speed up; if the electrical load is greater, the turbine will slow down.
Note: Load and gate position are entered in different parameter tables in HAMMER because they may not use the same time interval. HAMMER interpolates automatically as required. With the Load Rejection Operating Case, the wicket gate position (in the Operating Rule) must start at 100% and drop to 0%. To model a wicket gate that does not change position, enter a 0% point on the Operating Rule, after the end of the transient simulation.
Island Operation - Load Rejection can be used to model a turbine in "island" operation (it is the only source of a electricity for a small grid such as a village or an island) where you want to determine the maximum electrical load change that can be achieved within acceptable pressures. For example if there is a surge in electrical demand (load), you may want to simulate how the turbine reacts to this - how the speed changes. If a governor controls the wicket gates to compensate for the load change, you would model that manually with the "Pattern (Gate Opening)". Because the relative opening in the wicket gate operating rule pattern must drop to 0% when using the Load Rejection operating case, if you want to model a case where the wicket gate is assumed to not close at all or does not close all the way, you can still do that in the pattern table, but add extra rows at the end of the table that drop it to 0% after the end of your transient simulation duration.
If you want to see the speed return back to the nominal speed, you will need to determine how fast to close the wicket gates in order to prevent the speed increase, while also preventing any damaging transients as a result of the closure. You will also need to determine how quickly the wicket gates will be able to react to the electrical torque change (by way of the pattern).
Load Acceptance
Full load acceptance occurs when the turbine-generator unit is connected to the electrical grid. Transient pressures generated during full load acceptance can be significant but they are usually less severe than those resulting from full load rejection.
HAMMER assumes the turbine initially operates at no-load speed (NLS), and the turbine generates no electrical power. When the transient simulation begins, HAMMER assumes the electrical grid is connected to the output terminal of the generator and wicket gates have to be open as quickly as possible to meet the power demand, all without causing excessive pressure in the penstock.
Note that in this case, HAMMER assumes the turbine governor is ‘perfect.’ In other words the power produced by the turbine always equals the electrical load. Therefore the user doesn't need to enter an electrical load, just a curve of wicket gate position versus time, and the turbine's rated flow and head. Under the Load Acceptance case the turbine will always operate at its rated (or synchronous) speed.
When using Load Acceptance, you must enter the Flow (Rated) and Head (Rated) for the turbine. The transient solver needs these values into order to use the characteristic curve for the turbine during the transient simulation. Since the initial flow is zero for load acceptance, the "rated" head and flow input fields are used instead of the turbine curve, to represent the nominal operating point of the turbine when the gate is eventually fully open. This information should be available from the turbine manufacturer or you can obtain it by performing a steady state initial conditions run with the turbine open, and note the calculated head and flow from the "results" section of the properties, then set the turbine initial status to Closed and enter those values for the nominal operating point.
Load Variation
Load variation on the turbine-generator unit can occur due to the diurnal changes in electricity demand in the distribution grid. During load variation, the governor controls the wicket gate opening to adjust flow through the turbine so that the unit can match the electrical demand. The water column in the penstock and conduit system accelerates or decelerates, resulting in pressure fluctuations.
The transient pressures that occur during general load variation may not be significant from a hydraulic design perspective since they are often lower than the pressure generated during a full load rejection or emergency shutdown.
At steady-state, the turbine-generator system usually runs at full load with the wicket gates 100% open. The amount of electricity produced by the system depends on the flow through the wicket gates. A decrease in electrical load requires a reduction in the wicket gate opening to adjust the flow.
The wicket gate pattern must start at 100% and cannot drop below 30%.
Note that in this case, like in the case of the Load Acceptance operating case, HAMMER assumes the turbine governor is ‘perfect.’ Under the Load Variation case the turbine will always operates at its rated (or synchronous) speed.
Viewing Results
As with other elements in HAMMER, results for turbines can be viewed using the Transient Results Viewer. Profile animations will show how the pressure and hydraulic grade will change along a path and over the length of the simulation. The Time History tab will allow the user to view results for flow, hydraulic grade, pressure, air/vapor volume, as well as velocity and force, at points in the model. Locations will need to be added as report points to see the results at points in the model. In the Extended Node Data tab, the user can view a graph for speed or wicket gate opening for the turbine.
If a value was included for the "Report Period (Transient)”, the user can see select turbine results in the Transient Analysis Detailed Report. These results will include the time, the gate opening percentage, flow, speed, and head. This data can be copied into an Excel spreadsheet and graphed, if you want to see graphical results. As mentioned above, speed and wicket gate opening can be graphed from the Extended Node Data tab in the Transient Results Viewer.
Note that most of the default turbine characteristic curves (used by way of the selected "specific speed") do not have data for when the wicket gates are nearly closed. So, HAMMER performs a linear interpolation, and you will see text output results truncated for wicket gate positions below 20%. See: Why does my text output report for my turbine stop at the time when the gate is 20% open in HAMMER?
A Note on Simulating "Runaway Speed" or "Overspeed"
If you would like to model a runaway speed scenario in which the turbine gates do not close, see the following article. Speed can be graphed in the Extended Node Data tab of the Transient Results Viewer, when a number is entered in the Report Period field of the turbine.
Setting up a Runaway speed scenario for a turbine
A Note on Impulse or Pelton Wheel Turbines
An impulse turbine has one or more fixed nozzles through which pressure is converted to kinetic energy as a liquid (typically water) jet. The jet impinges on the moving plates of the turbine runner that absorbs virtually all of the moving water's kinetic energy. In practice, the most common impulse turbine is the Pelton wheel shown in the figure below.
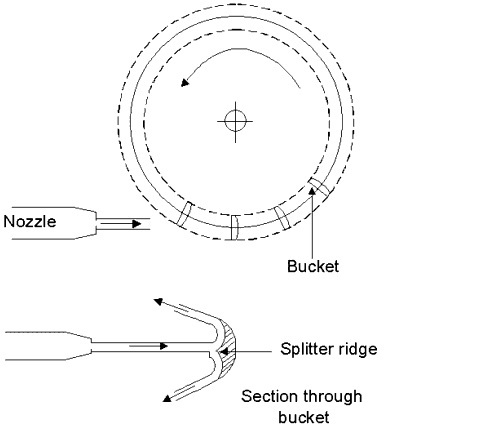
Its rotor consists of a circular disc with several "buckets" evenly spaced around its periphery. The splitter ridge in the center of each bucket divides the incoming jet(s) into two equal parts that flow around the inner surface of the bucket. Flow partly fills the buckets and water remains in contact with the air at ambient (or atmospheric) pressure.
It is important to note that the turbine element in HAMMER is not used to represent impulse turbines. Transients caused by impulse turbines can be approximated in HAMMER by using a Throttle Control Valve (TCV) or Discharge to Atmosphere element to represent the turbine nozzle.
An example of this setup would be to approximate the gate closure on the impulse turbine using a "Discharge to Atmosphere" (D2A) element. See the schematic below for one possible setup of the system:
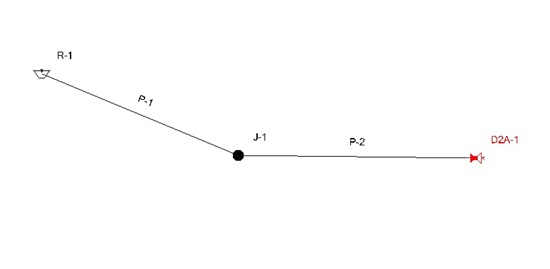
If you want to model the impulse turbine gate closing in 10 seconds, you would set the D2A property field "Discharge Element Type" to Valve with an initial status of Open. Then you would set "Time to Fully Open or Close" to 10 seconds.
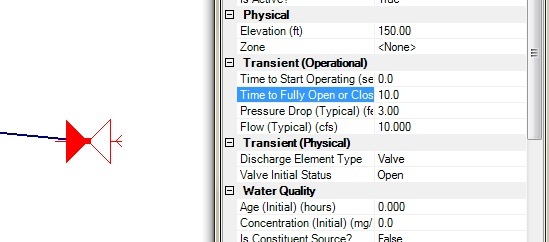
Note: remember to enter values for "Pressure Drop (Typical)" and "Flow (Typical)". The "Flow (Typical)" is simply the expected flow from the turbine. You can calculate the typical pressure drop using the orifice equation). More information on entering this information can be found in the Discharge to Atmosphere TechNote found here
If you want more control over the valve closure, you could use a Trottle Control Valve (TCV) element instead.
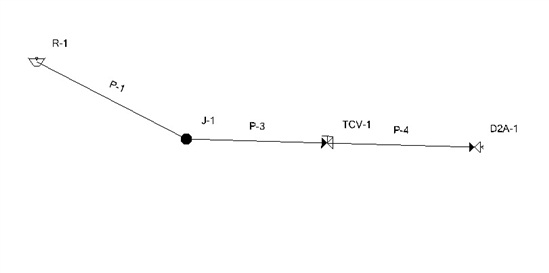
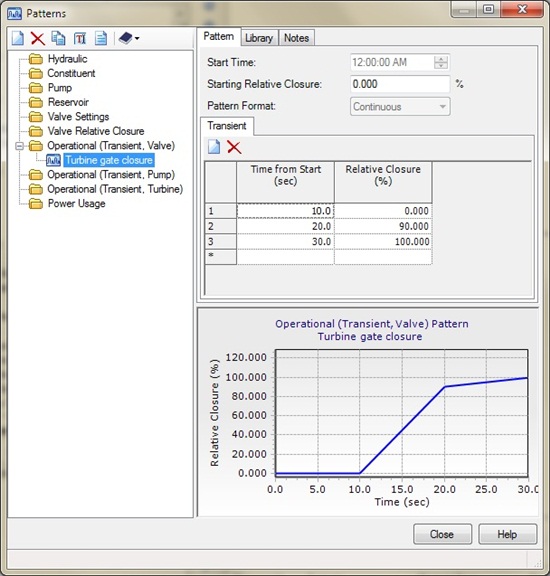
The TCV allows you to enter an Operating Rule that has curve of valve closure (or gate closure, for an impulse turbine) versus time. For example, you could have the gate close quickly until it 10% open, then close more slowly the rest of the way.
If you are modeling a Load Acceptance type case with for a Pelton turbine when using a TCV, you may end up with user notifications after computing the initial conditions stating that the Discharge to Atmosphere element has an demand that cannot be satisfied. The reason for this is that the TCV would be initial closed and the D2A would be set such that the program will see a demand on element. With the valve closed, there is no way to satisfy this demand. There are a couple of things that you can try in a case like this.
First, you can remove the TCV and use the valve feature on the D2A. This will use simplified closure characteristics, but this may be suitable for some modeling cases. See the information above for more information.
Second, rather than start with the TCV closed, start with the valve open. Set up the valve pattern so that it closes and remains closed for a time. How long will depend on how long it takes for the system to reach a new equilibrium and may take some trial and error. Once a new equilibrium is achieved, reopen the valve. The key results for your model will be during and after the valve reopening.
Third, you can set the Coefficient Type to "Valve Characteristic Curve" and set the valve status to Active. For the initial position of the valve, set this to be 100% closed. With this setting, you will see a very small amount of flow, but there will be no messages about the system being disconnected.
Lastly, you can ignore the user notifications. It will be very importance to make sure that the initial conditions results (such as flow and hydraulic grade) are correct and reasonable. If they are not, one of the options above will need to be implemented instead.
A Note on Pump-Turbines
HAMMER currently does not support modeling an emergency shutdown event for a pump turbine element (as typically the wicket-gate characteristics are built in) and the turbine element currently cannot start with reverse flow/speed. A pump-turbine option will be considered for a future release via Enhancement # 1060393.
As a workaround, you may want to try a sensitivity analysis with the valve characteristics, using a pump element plus TCV for the wicket gate. Try a range of configurations that you feel are within what would represent the characteristics of the wicket gate closure (discharge coefficient and valve characteristics curves). Compare the overall transient results for different configurations and if they do not vary significantly, then you may not need to bother trying to accurately model the pump-turbine wicket gates.
A Note on "Island Operation"
As seen further above, Load Rejection can be used to model a turbine in "island" operation (it is the only source of a electricity for a small grid such as a village or an island) where you want to determine the maximum electrical load change that can be achieved within acceptable pressures. For example if there is a surge in electrical demand (load), you may want to simulate how the turbine reacts to this - how the speed changes. If a governor controls the wicket gates to compensate for the load change, you would model that manually with the "Pattern (Gate Opening)". Because the relative opening in the wicket gate operating rule pattern must drop to 0% when using the Load Rejection operating case, if you want to model a case where the wicket gate is assumed to not close at all or does not close all the way, you can still do that in the pattern table, but add extra rows at the end of the table that drop it to 0% after the end of your transient simulation duration.
If you want to see the speed return back to the nominal speed, you will need to determine how fast to close the wicket gates in order to prevent the speed increase, while also preventing any damaging transients as a result of the closure. You will also need to determine how quickly the wicket gates will be able to react to the electrical torque change (by way of the pattern).
Modeling a turbine that stays closed
In some scenarios, one or more turbines may need to remain off (closed) for the entire transient simulation.
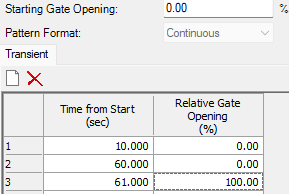
This can be accomplished by modeling the turbine as a load acceptance. To start the turbine in the off/closed position during the initial conditions, set the "Status (Initial)" to "Closed". If you want to have it off for the entire transient simulation, set the Operating Case to Load Acceptance, then assign a pattern with "Starting gate opening" as 0%, keep it as 0% for the entire duration, then add a row to the pattern table that has it rise to 100% after the end of the transient simulation (to avoid validation preventing you from running). For example the screenshot below would be used if the transient simulation was 60 seconds:
Another option is to model the turbine as a valve element such as a GPV, using the same flow vs. head "turbine curve" as the turbine, then set the initial status as closed and the pattern as Fixed.
A future version of HAMMER may include a "Fixed" operating case where you can model a turbine that starts closed and stays closed for the duration without having to specify a pattern. To express your interest in such a feature, post or vote on the Idea Portal. This will enable you to see the status of your idea, get votes from other users to help influence prioritization, and posts comments. See more here.
See Also
Protective Equipment FAQ
General HAMMER V8i FAQ
Convergence problems with turbine transient simulation
Modeling turbine instant load rejection with wicket gate starting less than 100% open
Why does my text output report for my turbine stop at the time when the gate is 20% open in HAMMER?